Table of Contents
Welcome back to another article in my Intro to Programming series.
In the previous article, I discussed data types in programming and I briefly went over the list of basic data types that you have available in Python.
- Intro to Programming: Why Beginners Should Start With Python
- Intro to Programming: What Are Different Data Types in Programming?
It's worth mentioning that the particular data types supported by each programming language vary a bit. The concept of data types, however, is universal.
In this article I begin diving into the Python data types to learn what they can do for you. I will say that a large part of beginner programming is getting familiar with the various data types available, so let's get started.
First, I'll cover numbers, as they are probably the most familiar and easiest to work with. You will remember from my article on data types that there are two basic types of numbers: integer numbers and floating-point numbers.
Integers are the easiest - these are whole numbers, so numbers that don't have a decimal part, such as 20, 10, and -5.
What Are Floating-Point Numbers?
Floating-point numbers are numbers that have a decimal component, so numbers such as 3.14, 2.73, etc. You may be wondering why this weird-term, "floating-point." The answer to that question is a bit more complicated, but if you're curious, it goes back to how computers actually represent numbers.
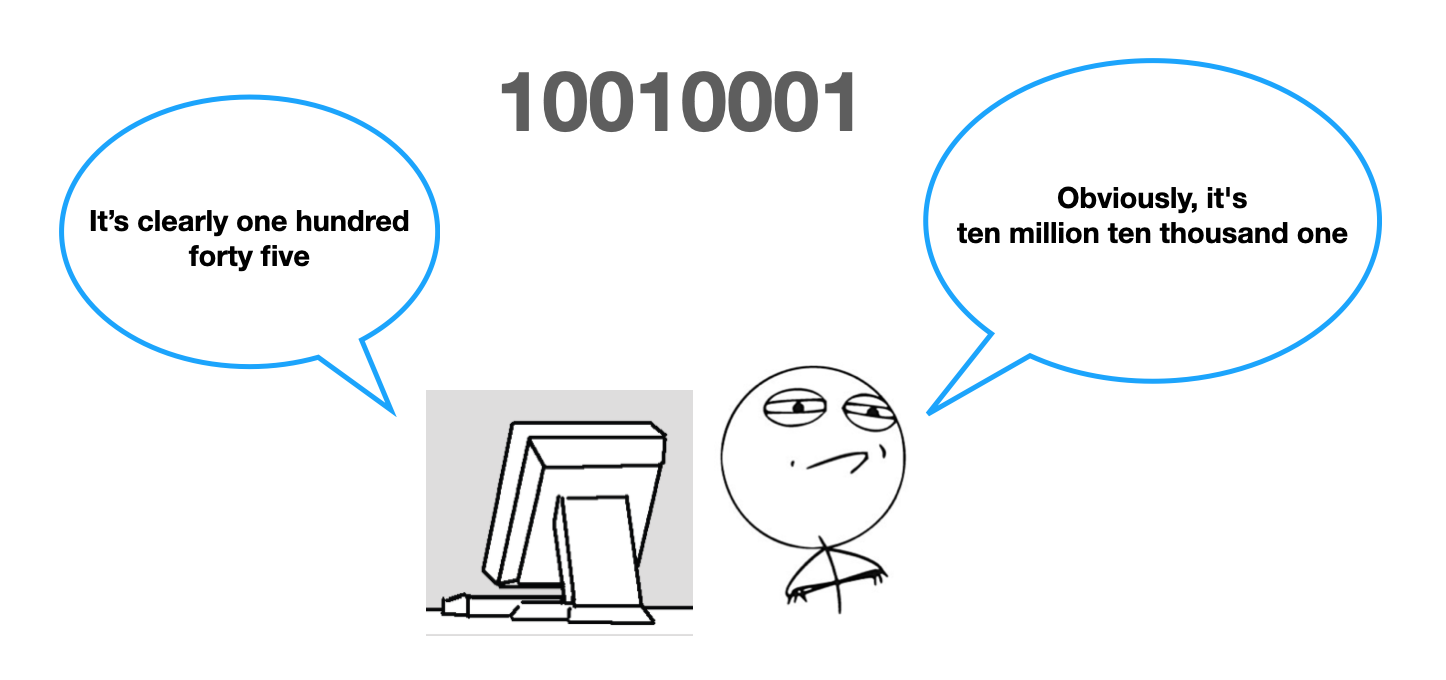
As you know, computers only operate with ones and zeros, so when a computer looks at any data, it only sees a sequence of zeros and ones. Like so:
10010001
In human speak, this number would be ten million ten thousand and one. In computer speak, it's actually the number 145 written in 8 bits.
Image Source: Edlitera
Imagine you're a computer. You can only use ones and zeros, and have a limited space in your memory. How do you represent numbers that have decimals?
Well, you simply decide where in that sequence of zeros and ones to "put" the decimal. Depending on what number you need to represent, the decimal point may be closer or farther from the beginning of the number.
10010.001
100.10001
This is called "floating," where the decimal point floats left and right to represent different numbers. Don't worry too much if this is a bit confusing, understanding this is not essential at this point in your learning and it will make more sense as you learn more programming.
How to Use Integers and Floating-Point Numbers in Python
Ok, so let's explore a bit what you can do with integers and floating-point numbers in Python. To do this, I'm going to start a Jupyter notebook.
For a refresher, follow this quick guide on how to start a new Jupyter notebook:
If you don't have Jupyter installed, read more here:
- Intro to Programming: How to Get Your Computer Ready to Run Python
- Intro to Programming: How to Write and Run Code
We're going to try out a few operations. For best outcomes, follow along on your computer.
- Note: In the examples below, the Python code is what follows the arrows: >>>. While the result of the code is printed immediately underneath without any leading >>>. This mimics the behavior you will encounter when using Jupyter notebooks or the Python command line.
How to Compute Addition in Python
Numbers in Python can be added using the + sign. In Python, + is called an operator. I'll talk more about operators in just a moment, but for now you can think of all mathematical signs (+, -, /, *, etc.) as operators.
Here's an example of addition in Python in Jupyter notebook:
>>> 2 + 4
6In the example above, 2 and 4 are called operands. Operands are the data on which operators act on. Pay attention for one moment to the data types involved: 2 and 4 are integers. The result, 6, is also an integer.
Compare that with the following example shown in Jupyter notebook:
>>> 2.0 + 4.0
6.0In this case, 2.0 and 4.0 are floating-point numbers. 6.0 is also a floating point number.
So far, you may notice that the result of an addition operation will have the same data type as the operands involved in the addition operation. But what happens when you add an integer to a floating-point number?
Here I'll add an integer to a floating-point number in Jupyter notebook:
>>> 2 + 4.0
6.0You get a floating-point number!
Why? Well, generally speaking, floating-point numbers have more precision. Therefore, when adding a number with less precision and a number with higher precision (i.e., with decimal points), Python will return a number with more precision.
This is very useful in situations like this shown in Jupyter notebook:
>>> 2 + 4.2
6.2Think about it: it would be quite unexpected to have 2 + 4.2 return 6.
Article continues below
Want to learn more? Check out some of our courses:
How to Compute Subtraction in Python
Numbers can be subtracted using the - operator.
Again, in the example below in Jupyter notebook, the minus is the operator and 2 and 10 are operands.
>>> 2 - 10
-8Of course, you can also subtract floating-point numbers:
>>> 2.1 - 10.1
-8.0And, you can mix and match integers and floating-point numbers:
>>> 2 - 10.1
-8.1How to Compute Multiplication in Python
Numbers can be multiplied using the * operator.
Here's an example of multiplication in Jupyter notebook:
>>> 2 * 2
4And, as you'd expect, this is the result:
>>> 2.1 * 2.1
4.41
But also, something you might not expect. Below is an actual result I got on my computer:
>>> 2.1 * 2.2
4.620000000000001That makes no sense, right?
If you do the math on a pocket calculator, you'll get 4.62, which is the correct answer. So why does Python return 4.620000000000001?
I mentioned earlier that floating-point numbers are represented using a fixed number of binary digits. Because you don't have infinite digits at your disposal, not all floating-point numbers can be represented accurately, so you will encounter rounding errors.
This is very important! Floating-point arithmetic in Python can be imprecise. As a word of caution, never use floating point numbers to represent quantities that need to be strictly accurate, such as money.
To do math with money in Python, for example, it is customary to work with cents, rather than full dollars. So instead of computing $1.5+$0.75, you would compute 150 + 75, with the understanding that the result will be in cents, not dollars.
For other quantities that need to be accurate, Python provides a more complex data type, called the decimal data type. I will be covering this in future blog posts.
How to Compute Exponents (Power) in Python
You can use the ** operator to compute powers. For example, you can compute 23 by writing 2 ** 3. This is equivalent to 2 * 2 * 2.
Here's an example of computing 2 ** 3 in Jupyter notebook:
>>> 2 ** 3
8Of course, you can also use floating-point numbers, but be aware of the potential rounding errors as shown:
>>> 2.1 ** 3
9.261000000000001How to Compute Division in Python
For division, you can use the / operator.
Here's an example of computing division in Python in Jupyter notebook:
>>> 5 / 2
2.5As you see above, 5 is an integer, 2 is an integer, but the result is 2.5, which is a float.
That makes sense. Let's try another one, shown here:
>>> 4 / 2
2.0Four divided by two is two. So why does Python return 2.0? Well, when using the / operator, Python 3 always returns the result of division as a floating-point number even if the result is a whole number.
What if you want the integer approximation of a division?
For this use case, Python provides the // operand, as shown:
>>> 2 // 3
0
Please note that when using the // operator, Python performs floor division. In other words, it rounds down the result to the nearest integer if the operands are integers.
When at least one of the operands is a floating-point number, something interesting happens. The result is a floating-point number, except the decimal part is always 0.
Here's an example:
>>> 7.0 // 3
2.0How to Compute Modulo (Mod) in Python
The modulo operator % allows us to calculate the remainder when you perform division shown here in Jupyter notebook:
>>> 5 % 3
2And you can verify that 5 = 3 * 1 + 2, where, of course, 2 is the remainder you get when dividing 5 by 3.
Similarly as before, whether the remainder is an integer or a floating-point number depends on the data types of the operands. For example:
>>> 5.0 % 3
2.0In the example above, because at least one of the operands 5.0 is a floating-point number, the remainder will also be a floating point number.
This modulo operator is actually pretty useful to programmatically answer a very simple question: is a number odd or even?
From math, you know that when you divide a number by 2, if the remainder is 1, then the number is odd, and if it is 0, then the number is even. you know that 15, for example, is odd.
Here's an example:
>>> 15 % 2
1And indeed, the remainder of dividing 15 by 2 is 1, so 15 is odd.
What about 20? You can again use the modulo operator and you get 0, so 20 is even, as shown here:
>>> 20 % 2
0This may again sound silly, because you can tell that by just looking at the number. But what if you had a list of 10 million numbers and you needed to count how many of them are even? Rather than doing it by hand, you'd write a program that would use the modulo operator to determine which ones are even, and count them.
How to Use Operator Precedence in Python
So far, you've only seen very simple calculations. However, in Python, you can have as many operands and operators as you want.
For example, shown here in Jupyter notebook:
>>> 15 + 2 * 10
35How does Python compute the result? Well, it first multiplies 2 by 10 and then it adds 15 to the result.
But how come it knows not to first add 15 and 2, and then multiply the result by 10? It knows because of built-in rules defining the order in which operators should be evaluated.
This is called operator precedence and it's exactly the same one you learned in math.
To refresh your memory, the order is as follows:
- Exponent (power)
- Multiplication
- Division
- Addition
- Subtraction
In other words, EMDAS.
What if you really do want to tell Python to first add 15 and 2, and then multiply the result by 10?
That's simple: use parentheses as shown here:
>>> (15 + 2) * 10
170
>>> (3 + 4) * (2 + 3)
35This works because parentheses are always evaluated first. So, to be thorough, the full operator precedence rule is as follows:
- Parentheses
- Exponent (power)
- Multiplication
- Division
- Addition
- Subtraction
To more easily remember this, you can use the PEMDAS acronym.
A Cheat Sheet of Operators and Operands For Python
Let's summarize what you've learned so far in a table:
| Operation | Operator | Operands | Result |
| x + y | + | x, y | Returns the sum of x and y. |
| x - y | - | x, y | Returns the result of subtracting y from x. |
| x * y | * | x, y | Returns the result of multiplying x by y. |
| x ** y | ** | x, y | Returns the result of raising x to the power of y (equivalent of multiplying x by x, y times). |
| x / y | / | x, y | Returns the result of dividing x by y. The result will always be a floating-point number (in Python 3 and above). |
| x // y | // | x, y | Divides x by y and rounds down the result to the nearest whole number. |
| x % y | % | x, y | Returns the remainder of dividing x by y. |
Image Source: Edlitera
In the table above, x and y can be any integer or floating point number.
That's it for numbers for now. In this blog post I showed you how to do very basic math using Python and you learned about the various operators you can use, such as the plus sign + for addition and star * for multiplication. This is very basic, but this is actually where computers got started and where they will forever be unmatched by any human being: they are very, very fast and accurate when it comes to math.
Thanks for reading!